سوالات
1.همه مقادیر ممکن برای عدد طبیعی b را پیدا کنید به طوری که کسر 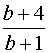 مساوی یک عدد صحیح باشد.
مساوی یک عدد صحیح باشد.
2. ثابت کنید کسر 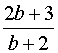 برای همه مقادیر صحیح
برای همه مقادیر صحیح 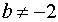 یک کسر ساده نشدنی است، یعنی برزگترین مقسوم علیه مشترک صورت و مخرج، ۱ است.
یک کسر ساده نشدنی است، یعنی برزگترین مقسوم علیه مشترک صورت و مخرج، ۱ است.
3. اتحادهای زیر را در نظر بگیرید و به وسیله آنها سه مساله زیر را حل کنید (معمولا به اولین اتحاد، اتحاد اویلر می گویند):
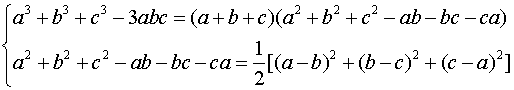
(الف) ثابت کنید اگر 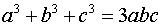 آن گاه
آن گاه 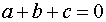 یا
یا 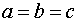 . عکس مطلب بالا را ثابت کنید؛ یعنی اگر
. عکس مطلب بالا را ثابت کنید؛ یعنی اگر 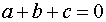 یا
یا 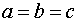 ، آن گاه خواهیم داشت
، آن گاه خواهیم داشت 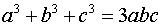 .
.
(ب) عبارت 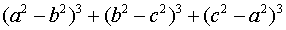 را به عوامل ضرب تجزیه کنید.
را به عوامل ضرب تجزیه کنید.
(ج) اگر a و b و c سه عدد مثبت باشند و 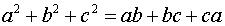 ، مقدار عبارت زیر را به دست آورید:
، مقدار عبارت زیر را به دست آورید:
4. نشان دهید که به ازای هر عدد صحیح n، 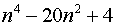 یک عدد اول نیست.
یک عدد اول نیست.
5. معادله ی زیر را حل کنید:
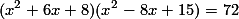
6. فرض کنید x، y و z سه عدد حقیقی باشند که x+y+z=0؛ ثابت کنید:
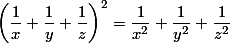
نتیجه بگیرید که برای هر سه عدد b، a و c که دو به دو متمایز باشند، داریم:
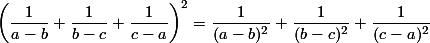
7. فرض کنید a عددی حقیقی باشد. ثابت کنید:
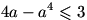
8. عبارت زیر را به صورت حاصل ضرب دو عبارت با درجه ی بیشتر از یک تجزیه کنید:
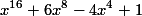
9.تساویهای زیر را در نظر بگیرید و قانونی کلی برای آن ها به دست آورید.
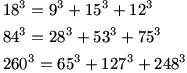
10. بین y، x یا z چه ارتباطی باید باشد تا تساوی زیر برقرار باشد:
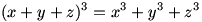
11. همه ی جواب های معادله ی زیر را بیابید:
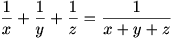
12. سعی کنید حداقل یک جواب در میان اعداد صحیح برای دستگاه معادله ی زیر پیدا کنید:
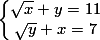
پاسخ ها
حل مساله ی 1:
اگر کسر را مساوی عدد طبیعی k فرض کنید، خواهیم داشت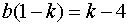 . حال با توجه به اینکه k نمی تواند مساوی 1باشد،طرف سمت چپ، منفی استو لذا k برابر است با 2 یا 3. با بررسی مختصر می توان دید که باید b=2.
. حال با توجه به اینکه k نمی تواند مساوی 1باشد،طرف سمت چپ، منفی استو لذا k برابر است با 2 یا 3. با بررسی مختصر می توان دید که باید b=2.
حل مساله ی 2:
فرض کنید صورت و مخرج مضرب یک عدد طبیعی مانند n باشند. لذا برای یک k از اعداد صحیح باید b+kn+1 نیز مضربیاز n باشد. در نتیجه b+1نیز مضربی از nاست. چون b+2مضربی از n است، لذا باید 1 نیز مضربی از nباشد. پس n=1.
حل مساله ی 3:
(الف)با توجه به اتحاد اول، اگر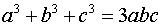 ، آنگاه سمت چپ اتحاد اول، صفر خواهد شد و در نتیجه در سمت راست یاپرانتز اول صفر است یاپرانتز دوم. حال با توجه به اتحاد دوم، مساله الف حل می شود.
، آنگاه سمت چپ اتحاد اول، صفر خواهد شد و در نتیجه در سمت راست یاپرانتز اول صفر است یاپرانتز دوم. حال با توجه به اتحاد دوم، مساله الف حل می شود.
(ب)توجه کنید که مجموع عبارات داخل پرانتز ها صفر است. حال از مساله الف و نیز اتحاد مزدوج استفاده کنید تا به عبارت زیر که جواب مساله است، برسید:
(ج) با توجه به اتحاد دوم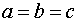 . بنابراین
. بنابراین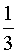 جواب مسالهاست.
جواب مسالهاست.
حل مساله ی 4:
می توان نوشت:
از طرف دیگربا حل معادلات ساده درجه 2 می توان نشان داد که
بنابر این،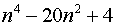 همواره مرکب است و عدد اولی نیست.
همواره مرکب است و عدد اولی نیست.
حل مساله ی 5:
ابتدا به مراحل زیر دقت کنید:
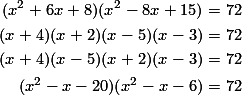
حال قرار دهید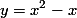 . بنابر این
. بنابر این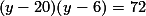 . با حل این معادله نسبت به مجهول y، به دست می آید: y=2 و y=24. حال با حل دو معادله ی دیگر، جواب ها عبارتند از:
. با حل این معادله نسبت به مجهول y، به دست می آید: y=2 و y=24. حال با حل دو معادله ی دیگر، جواب ها عبارتند از:
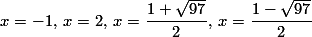
نکته:توجه کنید که بعد از تجزیه، دیده می شود که مجموع اعداد 2و3- و نیز مجموع اعداد 4 و 5- با یکدیگر برابر است. حال با دسته بندی مناسب و با یک تغییر متغیر، معادله به راحتی حل می شود.
حل مساله ی 6:
کافی است توجه کنید که بر اساس اتحاد مربع دو جمله ای:
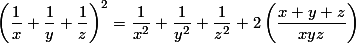
حل مساله ی 7:
نامساوی مساله را می توان به صورت زیر نوشت، که به وضوح درست است:
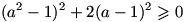
حل مساله ی 8:
به اتحاد زیر توجه کنید:
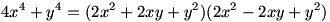
با استفاده از اتحاد بالا می توان نوشت:
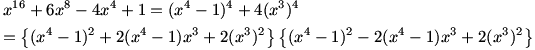
حل مساله ی 9:
قانون کلی عبارت است از
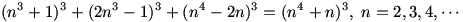
حل مساله ی 10:
می توان نوشت
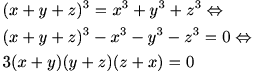
بنابر این برای برقراری تساوی باید x=-y یا x=-z یا y=-z.
حل مساله ی 11:
برای برقراری تساوی باید x=-y یا x=-z یا y=-z زیرا
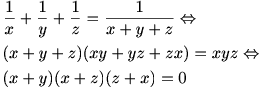
حل مساله ی 12:
قرار دهید
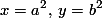
که a و b را مثبت فرض خواهیم کرد. معادله ی بالا را از پایینی کم کنید. با این کار می توان نوشت:
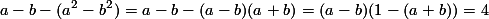
حالت های مختلفی را که حاصل ضرب دو عدد صحیح، 4 می شود در نظر بگیرید (مانند 2*2 یا ضرب 4-*1-). با امتحان کردن این موارد به دست می آید: a=2 و b=3. بنابر این x=4 و y=9.
منبع
این مقاله در سایت علمی
رایشمند منتشر شده است. خوشحال میشویم اگر
دیدگاه و نظر خود را درباره این موضوع با ما و دیگر خوانندگان در میان بگذارید.